Question

In their never-ending quest to siphon the money from your wallet, the carnival operators have come up with a new game: Super-Mega-Chuck-A-Luck! Here you roll seven dice, with payoffs as follows: A grand prize of $5,000 if you roll seven of a kind $500 if you roll six of a kind $50 if you roll five of a kind What is the expected value of Super-Mega-Chuck-A-Luck?

Answer 1

The expected value is $0.035

Explanation:

expected of outcome for each dice = 1,

each dice has 6 sides ⇒ total number of possible outcome per dice = 6

seven of a kind = $5,000, six of a kind = $500, five of a kind = $50

Probability = (expected outcome ÷ total number of possible outcome) ^ number of dice

Pr =
`((E))/(T)^(n)`

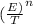
seven of a kind ⇒ all 7 dice have the same number

Pr (seven of a kind) =
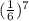`((1)/(6))^(7)` = 0.00000357

six of a kind ⇒ all 6 dice have the same number

Pr (six of a kind) =
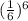`((1)/(6))^(6)` = 0.0000214

five of a kind ⇒ all 5 dice have the same number

Pr (five of a kind) =
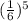`((1)/(6))^(5)` = 0.000129

EV = ∑P(
`X_(i)`) *

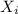EV = 5,000 * 0.00000357 + 500 * 0.0000214 + 50 * 0.000129

EV = 0.01785 + 0.0107 + 0.00645

EV = $0.035

The chances of winning is less than 1%. This is a very bad risk to take, do not let the carnival operators siphon the money in your wallet