Question

Two​ researchers, Jaime and​ Mariya, are each constructing confidence intervals for the proportion of a population who is​ left-handed. They find the point estimate is 0.18. Each independently constructed a confidence interval based on the point​ estimate, but​ Jaime's interval has a lower bound of 0.174 and an upper bound of 0.274​, while​ Mariya's interval has a lower bound of 0.115 and an upper bound of 0.245. Which interval is​ wrong? Why?

Answer 1

Jaime's confidence interval is incorrect.

Explanation:

The (1 - α)% confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

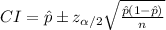
Here,

`\hat p` = sample proportion

A point estimate of a parameter (population) is a distinct value used for the estimation the parameter (population). For instance, the sample mean
`\bar x` is a point estimate of the population mean μ.

Similarly the sample proportion
`\hat p` is the point estimate of the population proportion.

It is provided that the point estimate of the proportion of left-handed people is,
`\hat p` = 0.18.

In case of confidence intervals, the central point or the value at the center of the interval is the point estimate.

So, the central point of the confidence interval for population proportion is the sample proportion, i.e.

`\hat p=(LL+UL)/(2)`

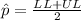
The confidence interval for population proportion computed by Jaime is:

CI₁ = (0.174, 0.274)

Compute the center of CI₁ as follows:

`\hat p=(LL+UL)/(2)`

`=(0.174+0.274)/(2)`

`=0.224`

`\\eq 0.18`

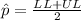
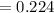
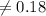
The confidence interval for population proportion computed by Mariya is:

CI₂ = (0.115, 0.245)

Compute the center of CI₂ as follows:

`\hat p=(LL+UL)/(2)`

`=(0.115+0.245)/(2)`

`=0.18`

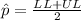
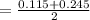
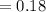
Jaime's confidence interval for population proportion is not centered at the point estimate, 0.18.

Thus, Jaime's confidence interval is incorrect.