Answer:
Measure of
 to nearest tenth of a degree is
to nearest tenth of a degree is
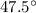 .
.
Explanation:
Diagram of given scenario is shown below.
Given that,
A right angle triangle
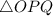 . Base of triangle is
. Base of triangle is
 .
.
Perpendicular side of triangle is
 and Hypotenuse side of triangle is
and Hypotenuse side of triangle is
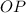 .
.
In
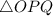 ,
,
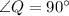 ,
,
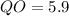 and
and
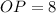 .
.
Now, Using Trigonometry ratio:

So, Substituting the values of perpendicular and hypotenuse we get:
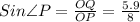
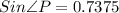 ⇒
⇒
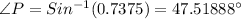
Therefore, Measure of
 to nearest tenth of a degree is
to nearest tenth of a degree is
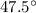 .
.