Question

Zed, Roy and Max had 231 game cards altogether. Zed gave 1/6 of his card to Roy and 1/4 of his cards to Max. In the end, all of them had the same number of cards,

A. How many cards did Zed have at first?

B. How many cards did each boy have in the end?

Answer 1

The answers are:

A. Zed had 132 cards at first

B. in the end, each boy had 77 cards

Explanation:

Let the original number of cards be

Zed = a ; Roy = b ; Max = c

we are told that:

a + b + c = 231 . . . . . . .(1) (Zed, Roy and Max had 231 game cards altogether)

Next, we are told that Zed gave 1/6 of his card to Roy and 1/4 of his card to Max. After this distribution, the new number of cards each of them had was:

Roy = 1/6 of Zed's cards + his original number of cards

`Roy=((1)/(6) *a) + b= (a)/(6) + b\\\\Roy = (a)/(6)+b`

Max = 1/4 of Zed's cards + his original number of cards

`Max= ((1)/(4) * a) + c = (a)/(4) + c\\\\Max = (a)/(4) + c`

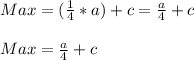
Zed = original no. of cards - ( amount given to Roy + amount given to Max)

`Zed = a - ((a)/(4) + (a)/(6) )= a - ((3a+2a)/(12) )\\= a - ((5a)/(12) )\\= (a)/(1)-(5a)/(12) = (12a-5a)/(12) = (7a)/(12) \\\\Zed = (7a)/(12)`

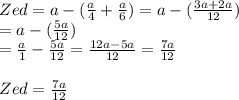
Next, we are told that after Zed distributed his cards, all of them had the same number of cards. We can represent this as:

For the new number of cards = Zed's = Roy's = Max's

Therefore:

`(7a)/(12) = ((a)/(6)+b) = ((a)/(4) + c)`

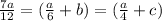
This also means that:

`(7a)/(12) = (a)/(6)+b\\b = (7a)/(12)-(a)/(6) = (7a-2a)/(12) = (5a)/(12) \\\\b= (5a)/(12)`

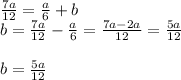
and

`(7a)/(12) = (a)/(4) + c\\c = (7a)/(12)- (a)/(4) = (7a-3a)/(12) = (4a)/(12)= (a)/(3)\\\\c = (a)/(3)`

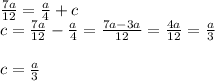
Next, we will replace the values of 'b' and 'c' gotten above in equation 1

a + b + c = 231 . . . . . . .(1)

where;
`b = (5a)/(12) ; c = (a)/(3)`

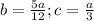
Therefore equation (1) becomes

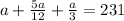`a + (5a)/(12) + (a)/(3) = 231` (solving for a)

`(12a+5a+4a)/(12) = 231\\ \\(21a)/(12) = 231\\`

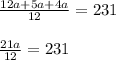
Next, multiplying both sides by 12 ;

`21a= 231*12 = 2772\\21a = 2772\\ \\a = (2772)/(21) = 132\\\\a = 132`

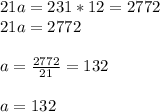
Therefore, Zed's original number of cards (a) = 132

B. In the end, we are told that they each have an equal number of cards.

since the total number of cards is 231, if we divide this by 3, then we will get the number of cards for each of the boys. This is shown as follows:

each of the boys have ; Total no. of cards ÷ No. of boys

= 231 ÷ 3 = 77 cards each