Question

Jane is playing a game in which he spins a spinner with 6 equal-sized slices numbered 1 through 6. The spinner stops on a numbered slice at random This game is this: Jane spins the spinner once. She wins $1 if the spinner stops on the number 1, $4 if the spinner stops on the number 2, $7 if the spinner stops on the number 3, and $10 if the spinner stops on the number 4. She loses $8.75 if the spinner stops on 5 or 6.

Find the expected value of playing the game.

Answer 1

The expected value of playing the game is $0.75.

Explanation:

The expected value of a random variable is the weighted average of the random variable.

The formula to compute the expected value of a random variable X is:

`E(X)=\sum x\cdot P(X=x)`

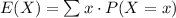
The random variable X in this case can be defined as the amount won in playing the game.

The probability distribution of X is as follows:

Number on spinner: 1 2 3 4 5 6

Amount earned (X): $1 $4 $7 $10 -$8.75 -$8.75

Probability: 1/6 1/6 1/6 1/6 1/6 1/6

Compute the expected value of X as follows:

`E(X)=\sum x\cdot P(X=x)`

`=(1* (1)/(6))+(4* (1)/(6))+(7* (1)/(6))+(10* (1)/(6))+(-8.75* (1)/(6))+(-8.75* (1)/(6))`

`=(1)/(6)+(4)/(6)+(7)/(6)+(10)/(6)-(8.75)/(6)-(8.75)/(6)`

`=(1+4+7+10-8.75-8.75)/(6)`

`=0.75`

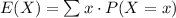
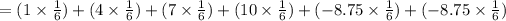
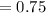
Thus, the expected value of playing the game is $0.75.