Question

At age, 18 you start to work for a company and are offered two rather fanciful retirement options.

Retirement Option 1:When you retire, you will be paid a lump sum of $15,000 for each year of service.
Retirement Option 2:When you start to work, the company will deposit $10,000 into an account that pays 9.6% interest compounded monthly. When you retire, the account will be closed and the balance given to you.
How much will you have under the second plan at age 55? (Round your answer to the nearest cent.)

Answer 1

The answer is $343,934.91 (to the nearest cent.)

Step-by-step explanation:

For the second option, we will calculate the future value of an amount invested for a period of time, which is compounded periodically, using the formula:

`FV=PV(1+(r)/(n) )^(n*t)`

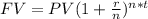
where:

FV = future value = ?????

PV = present value = $10,000

r = interest rate in decimal = 9.6% = 9.6/100 = 0.096

n = frequency of compounding in a year = monthly = 12

t = time = 18 years to 55 years = 55 - 18 = 37 years, \

Therefore:

`FV=PV(1+(r)/(n) )^(n*t)`

`10,000(1+(0.096)/(12) )^((12*37))\\= 10,000*(1.008)^(444) \\= 10,000 * 34.39349075 = 343,934.908`

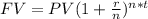
∴ FV = $343,934.91 (to the nearest cent.)

Note that rounding off to the nearest cent means rouding off to the nearest hundredth or to two decimal places.

Therefore under the second plan, at age 55, he will be given $343,934.91.

Also, if we are asked to compare both options to choose which is better,

for option 1 which will pay him $15,000 for each year of service (that is from 18 years to 55 years):

Years of service = 37 years

lump sum per year = $15,000

Therefore total amount from option 1 = 15,000 × 37 = $555,000

Therefore, at age 55, option 1 is better than option 2.