Question

After some food is introduced into a petri dish containing bacteria, the number of bacteria in the dish increases rapidly.The relationship between the elapsed time, t, in seconds, since the food was introduced, and the total number of bacteria, N(t) is modeled by the following function: N(t)=1000(8)t

​
​Complete the following sentence about the rate of change of the bacterial culture.Round your answer to two decimal places.
The number of bacteria is doubled every
seconds.

Answer 1

the bacteria doubled every 0.33 seconds

Explanation:

got this from khan academia

Answer 2

`2000=1000 (8)^t`

If we dicide both sides by 1000 we got:

`2 = 8^t`

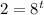
Now we can apply natural log on both sides and we got:

`ln (2)= ln (8^t) = t ln(8)`

And solving for t we got:

`t = (ln(2))/(ln(8))=0.333`

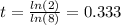
So then we can conclude that every 0.333 seconds the amount of bacteria is doubled under the model assumed.

The number of bacteria is doubled every 0.333 seconds

Explanation:

For this case we have the following model given for the number of bacteria after t seconds:

`N(t) = 1000 (8)^t`

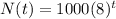
We want to find the time that is required to double the number of bacteria. If we analyze the function we see that the initial amount for t=0 is 1000. And if we want to double this amount we need to have 2000. And using this we have:

`2000=1000 (8)^t`

If we dicide both sides by 1000 we got:

`2 = 8^t`

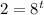
Now we can apply natural log on both sides and we got:

`ln (2)= ln (8^t) = t ln(8)`

And solving for t we got:

`t = (ln(2))/(ln(8))=0.333`

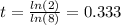
So then we can conclude that every 0.333 seconds the amount of bacteria is doubled under the model assumed.

The number of bacteria is doubled every 0.333 seconds