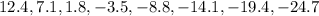Answer:
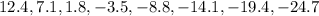
Explanation:
If the sequence has six arithmetic means between 12.4 and -24.7.
Let the sequence be:
12.4,a,b,c,d,e,f, -24.7
It means we have:
First term, a=12.4
Eighth Term =-24.7
The nth term of an arithmetic sequence is obtained using the formula below.
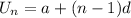
Therefore:
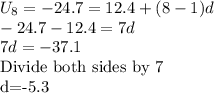
Therefore:

The sequence is: