Question

A room is 5m by 3m and has a height of 3.5m. Find the distance from a comer point on the floor to the opposite comer of the ceiling.

Answer 1

Approximately 6.8m

Explanation:

We can picture this problem by drawing a rectangular prism with a width of 5m, a depth of 3m, and a height of 3.5m. To find the length from one corner of the floor to the opposite corner of the floor, we can use the pythagorean theorem and plug in the width and depth of the room for a and b:

`5^(2)+3^(2)=c^(2)`

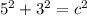
And now we can solve for c...

`34 = c^(2)`

`√(34)=\sqrt{c^(2)}`

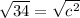
c = 5.831m

Now that we have the length from corner to corner across the floor, we can use the pythagorean theorem again, this time using the length from corner to corner across the floor we just derived and the height of the room:

`5.831^(2) + 3.5^(2)=c^(2)`

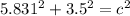
And now we can solve for c again...

`46.25=c^(2)\\√(46.25)=√(c^2)`

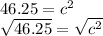
c = 6.8m