Question

Fifteen years ago, you deposited $12,500 into an investment fund. Five years ago, you added an

additional $20,000 to that account. You earned 8%, compounded semi-annually, for the first ten years,
and 6.5%, compounded annually, for the last five years.
Required:
a) What is the effective annual interest rate (EAR) you would get for your investment in the first 10
years? (2 marks)
b) How much money do you have in your account today? (4 marks)
c) If you wish to have $85,000 now, how much should you have invested 15 years ago? (4 marks)

Answer 1

a) 8.16%

b) $65,762.50

c) $39,701.07

Explanation:

Given:

15 years ago, Initial investment = $12500

5 years ago, Investment = $20000

Nominal interest = 8% semi annually for first 10 years

Interest2= 6.5% compunded annually for last five years

a) for the effective annual interest rate (EAR) in the first 10 years, let's use the formula:

[1+(nominal interest rate/number of compounding periods)]^ number of compounding periods-1

`EAR = [1 + ((0.08)/(2))]^2 - 1`

`= (1 + 0.04)^2 - 1`

`= (1.04)^2 - 1`

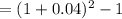
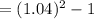
= 1.0816 - 1

= 0.0816

= 8.16%

The effective annual interesting rate, EAR = 8.16 %

b) To find the amount in my account today.

Let's first find the amount for $12500 for 10 years compounded semi annually

= 12,500 +( 12,500 * 8.160% * 10)

= $ 22,700

Let's also find the amount for $32,500($12,500+$20,000) for 5 Years compoundeed annually

$32,500 + ($32,500 * 6.5% *5)

= $ 43,062.50

Money in account today will be:

$22,700 + $43,062.50

= $65,762.50

c) Let's the amount I should have invested to be X

For first 10 years at 8.160%, we have:

Interest Amount = ( X * 8.160% * 10 ) = 0.8160 X

For next 5 years at 6.5%, we have:

Interest Amount = (X * 6.5% * 5) = 0.325 X

Therefore the total money at the end of 15 Years = 85000

0.8160X + 0.3250X + X = $85,000

= 2.141X = $85,000

X = 85,000/2.141

X = 39,701.074 ≈ $39,700

If I wish to have $85,000 now, I should have invested $39,700 15 years ago