Answer:
The probability that the coin lands heads up once and tails up twice is .375, or 3/8.
Explanation:
Check the conditions for a binomial distribution problem:
- Define success = heads and failure = tails.
- The number of trials is fixed; n = 3.
- Each coin flip is independent of the other.
- Probability p = .5 of getting either heads or tails.
We need to use combinations to determine the probability of getting one success (one head) and two failures (two tails).
The combination would be 3 choose 1:
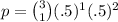 .
.
There is one success and two failures, denoted by the superscripts above the probability p = .5.
Use a calculator to evaluate and we get:
The probability that the coin lands heads up once and tails up twice is .375, or 3/8.