Question

Seth’s parents gave him $5000 to invest for his 16th birthday. He is considering two investment options. Option A will pay him 4.5% interest compounded annually. Option B will pay him 4.6% compounded quarterly. 1) Write a function of option A and option B that calculates the value of each account after n years. 2) Seth plans to use the money after he graduates from college in 6 years. Determine how much more money option B will earn than option A to the nearest cent. 3) Algebraically determine, to the nearest tenth of a year, how long it would take for option B to double Seth’s initial investment.

Answer 1

1) Function of option
`,A=5000(1.045)^t`

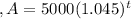
option
`B =5000(1.0115)^(4t)`.

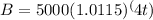2)After 6 years, how much more money option B will earn than option A is 67.57 $.

3)It would take 15 years for option B to double Seth’s initial investment.

Explanation:

Given:

Initial Investment=5000$

Option A(rate)= 4.5% .....annually

Option B(rate)=4.6 %..........Quarterly

To Find:

1)Write a function of option A and option B

2)After 6 years, how much more money option B will earn than option A

3) how long it would take for option B to double Seth’s initial investment.

Solution:

To write the function use formula of compound interest as ,

`A=P(1+r)^t`

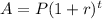
For option A ,P=5000$ r=4.5 % annually

`A=5000(1+0.045)^t`

`A=5000(1.045)^t`

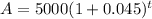
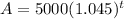
For Option B ,P=5000$ r=4.6 % Quarterly

`B=5000(1+0.046/4)^(4t)`

`B=5000(1+0.0115)^(4t)`

`B=5000(1.0115)^(4t)`

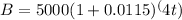
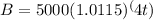
2)After 6 years, how much more money option B will earn than option A,

Here t=6 so Above equation will be ,

`A=5000(1.045)^t`

`A=5000(1.045)^6`

`A=6511.30 $` $

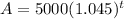
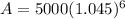
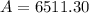For Option B

B=5000(1.0115)^ 4*6

`B=5000(1.0115)^(24)`

`B=6578.87` $

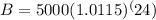
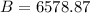B will earn more money as

therefore B -A

`=6578.67 -6511.30`

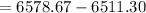
=67.57 $

3)how long it would take for option B to double Seth’s initial investment

By doubling the invest i.e for 10000 $ how much time will required.

So B=10000$ , P=5000$ and r= 4.5 % Quarterly

10000=5000(1.0115)^4t

2=(1.0115)^4t

Using the definition of the logarithm as ,

4t=Log2 with base 1.0115............. use this in calculator

4t=60.62

t=15.155 years

i.e, t=15 years.