Answer:
Q = 2.3 * 10⁻⁴ Gy
Step-by-step explanation:
The mass of the human body, M = 70 kg
Mass of potassium,
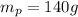
Atomic mass of potassium, MM = 39.1 g/mol
The half life of the isotope 40K,
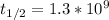
Number of moles of potassium,
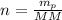
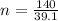
n = 3.58 mols
Let the number of atoms in the potassium be N
Number of mols of potassium,
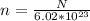
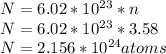
The 40K isotope has a natural abundance of 0.012% = 0.00012
That means the number of atoms originally in the 40K isotope is,
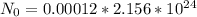
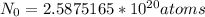
Number of atoms remaining after decay
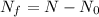
Decay constant,
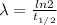
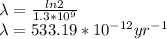
The question is asking for the yearly dose, i.e t = 1 yr
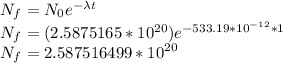
The number of 40K atoms decaying in 1 yr =
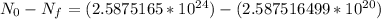
The number of 40K atoms decaying in 1 yr = 1 * 10¹¹ atoms
1 40K atom deposits 1.0MeV of energy into the body
1 * 10¹¹ atoms will deposit 1 * 10¹¹MeV of energy into the body = 10¹⁷ eV
1 eV = 1.6 * 10⁻¹⁹ Joules
10¹⁷ eV = (10¹⁷)*(1.6 * 10⁻¹⁹) Joules
10¹⁷ eV = 0.016 J
The amount of dose a typical body receives in Gy = 0.016/70
The amount of dose a typical body receives in Gy = 2.29 * 10⁻⁴