Answer:
i. The area of the entire circle is approximately 113 squared units.
ii. Area of the sector ACB is approximately 28 squared units.
iii. Area of the shaded region is approximately 14 squared units.
Explanation:
a. Area of a circle =


where r is the radius
The area of the entire circle =


=
 ×
×

=
 × 36
× 36
= 36
 squared units
squared units
= 113.143 squared units
The area of the entire circle is approximately 113 squared units.
b. Area of the sector ACB = (θ ÷ 2
 ) ×
) ×


= (θ ÷ 2
 ) × 36
) × 36

But, θ =
 rad. So that:
rad. So that:
Area of the sector ACB = (
 ÷ 2
÷ 2
 ) × 36
) × 36

= 9
 squared units
squared units
= 28.286 squared units
Area of the sector ACB is approximately 28 squared units.
c. Area of the shaded region = Area of triangle CDE
Area of triangle =
 × base × height
× base × height
Draw a perpendicular bisector of DE from C, then apply Pythagoras theorem so that:
h =

=
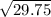
= 5.453 units
Thus,
Area of the shaded region =
 × 5 × 5.453
× 5 × 5.453
= 13.633 squared units
Area of the shaded region is approximately 14 squared units.