Answer:
b.
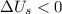
e.

Step-by-step explanation:
We are given that
Spring constant=k
Angle=

Mass=m
Distance=d
Distance=

Initial potential energy of spring=

Final potential energy of spring=0
Final potential energy of system=mgd
Initial mechanical energy of system=Initial K.E+Initial P.E=0+0=0
Final mechanical energy of the system=Kinetic energy+Potential energy=0+mgd
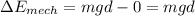 >0
>0

Option b and e are true.