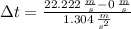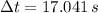Question

The sports car has a mass of 1.5 Mg Mg and a center of mass at G. Determine the shortest time it takes for it to reach a speed of 80 km/h km/h, starting from rest, if the engine only drives the rear wheels, whereas the front wheels are free rolling. The coefficient of friction between the wheels and road is μ=0.2μ=0.2. Neglect the mass of the wheels for the calculation.

Answer 1

`\Delta t = 17.041\,s`

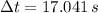
Step-by-step explanation:

The figure of the problem is included below as attachment. The equations of equilibrium are presented below:

`\Sigma F_(x) = -\mu\cdot N_(1) = m\cdot a`

`\Sigma F_(y) = N_(1) + N_(2) - m\cdot g = 0`

`\Sigma M_(G) = N_(1)\cdot x_(1) - N_(2)\cdot x_(2) - \mu\cdot N_(1)\cdot y_(1) = 0`

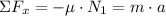
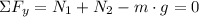
The system of equations are:

`-0.2\cdot N_(1) = (1500\,kg)\cdot a`

`N_(1) + N_(2) - (1500\,kg)\cdot \left(9.807\,(m)/(s^(2))\right) = 0`

`N_(1) \cdot [(0.75\,m)-0.2\cdot (0.35\,m)] - N_(2)\cdot (1.25\,m) = 0`

The solution of the system is:

`N_(1) = 9780.918\,N`,
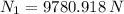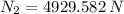`N_(2) = 4929.582\,N` and
`a = - 1.304\,(m)/(s^(2))`

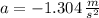
The shortest time to reach a speed of 80 km/h is:

`\Delta t = (22.222\,(m)/(s)-0\,(m)/(s))/(1.304\,(m)/(s^(2)) )`

`\Delta t = 17.041\,s`