Answer:
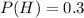
And the probability of tails

The probability of win in both tosses assuming the condition given that the game in fact go to overtime and that the events are independnet would be:
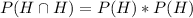
And replacing we got
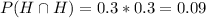
And then the probability of not win in both games by the complement rule is
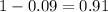
So the best answer would be:
b.91
Explanation:
For this case we know that the team always select the option heads for the game and for overtime, and we know that the coin is biased with the probability of heads given by:
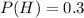
And the probability of tails

The probability of win in both tosses assuming the condition given that the game in fact go to overtime and that the events are independnet would be:
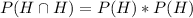
And replacing we got
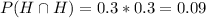
And then the probability of not win in both games by the complement rule is
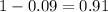
So the best answer would be:
b.91