Answer:
(a) The proportion of women who are tested, get a negative test result is 0.82.
(b) The proportion of women who get a positive test result are actually carrying a fetus with a chromosome abnormality is 0.20.
Explanation:
The Bayes' theorem states that the conditional probability of an event E
 , of the sample space S, given that another event A has already occurred is:
, of the sample space S, given that another event A has already occurred is:
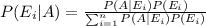
The law of total probability states that, if events E₁, E₂, E₃... are parts of a sample space then for any event A,
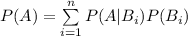
Denote the events as follows:
X = fetus have a chromosome abnormality.
Y = the test is positive
The information provided is:
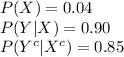
Using the above the probabilities compute the remaining values as follows:

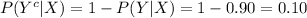
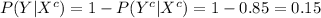
(a)
Compute the probability of women who are tested negative as follows:
Use the law of total probability:
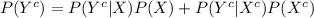
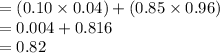
Thus, the proportion of women who are tested, get a negative test result is 0.82.
(b)
Compute the value of P (X|Y) as follows:
Use the Bayes' theorem:
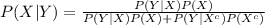
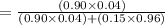
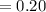
Thus, the proportion of women who get a positive test result are actually carrying a fetus with a chromosome abnormality is 0.20.