Question

A man invests his savings in two accounts, one paying 6% and the other paying 10% simple interest per year. He puts twice as much in the lower-yielding account because it is less risky. His annual interest is $6600 dollars. How much did he invest at each rate?

Answer 1

Let x represent amount invested in the higher-yielding account.

We have been given that a man puts twice as much in the lower-yielding account because it is less risky. So amount invested in the lower-yielding account would be
`2x`.

We are also told that his annual interest is $6600 dollars. We know that annual interest for one year will be principal amount times interest rate.

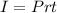`I=Prt`, where,

I = Amount of interest,

P = Principal amount,

r = Annual interest rate in decimal form,

t = Time in years.

We are told that interest rates are 6% and 10%.

`6\%=(6)/(100)=0.06`

`10\%=(10)/(100)=0.10`

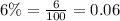
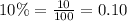
Amount of interest earned from lower-yielding account:
`2x(0.06)=0.12x`.

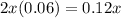Amount of interest earned from higher-yielding account:
`x(0.10)=0.10x`.

`0.12x+0.10x=6600`

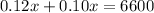
Let us solve for x.

`0.22x=6600`

`(0.22x)/(0.22)=(6600)/(0.22)`

`x=30,000`

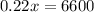
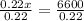
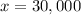
Therefore, the man invested $30,000 at 10%.

Amount invested in the lower-yielding account would be
`2x\Rightarrow 2(30,000)=60,000`.

Therefore, the man invested $60,000 at 6%.