Question

The authors of a paper presented a correlation analysis to investigate the relationship between maximal lactate level x and muscular endurance y. The accompanying data was read from a plot in the paper.

x: 400 740 770 810 850 1035 1190 1240 1290 1390 1475 1480 1505 2200
y: 3.80 4.10 4.80 5.30 3.90 3.40 6.20 6.88 7.55 4.95 7.90 4.45 6.70 8.90

Sxx = 2,648,130.357, Syy = 36.7376, Sxy = 7408.225.

a. Compute the value of the sample correlation coefficient, r. Round your answer to four decimal places.
b. Calculate the test statistic and determine the P-value. (Round your test statistic to two decimal places and your P-value to three decimal places.)

Answer 1

a) Sample correlation coefficient, r = 0.7411

bi) test statistic, t = 4.102

bii) P-value = 0.000736

Explanation:

a) The formula for the sample correlation coefficient is given by the formula:

`r = \frac{S_(xy) }{\sqrt{S_(xx) S_(yy) }} }`

`S_(xx) = 2,648,130.357\\S_(yy) = 36.7376,\\S_(xy) = 7408.225`

`r = (7408.225)/(√(2648130.357*36.7376) )`

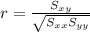
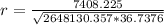
r = 0.7511

b)

i) formula for the test statistic is given by the formula:

`t = \frac{r√(n-1) }{\sqrt{1 - r^(2) } }`

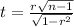
sample size, n = 4

`t = \frac{0.7511√(14-1) }{\sqrt{1 - 0.7511^(2) } }`

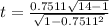
t = 4.102

ii) Degree of freedom, df = n -2

df = 14 -2

df = 12

The P-value is calculate from the degree of freedom and the test statistic using excel

P-value =(=TDIST(t,df,tail))

P-value = (=TDIST(4.1,12,1)

P-value = 0.000736