Question

The​ quality-control manager at a compact fluorescent light bulb​ (CFL) factory needs to determine whether the mean life of a large shipment of CFLs is equal to 7520 hours. The population standard deviation is 1 comma 120 hours . A random sample of 64 light bulbs indicates a sample mean life of 7 comma 324 hours.

Answer 1

The mean life span of the sample is approximately 10,246 hours.

Explanation:

plato

Answer 2

The mean life of a large shipment of CFL bulbs is equal to 7,520 hours.

Explanation:

The quality control manager wants to determine whether the mean life of a large shipment of CFL bulbs is equal to 7,520 hours.

The quality control manager can use a one-sample test to determine whether the mean life is 7,520 hours or not.

The hypothesis can be defined as follows:

H₀: The mean life of a large shipment of CFL bulbs is equal to 7,520 hours, i.e. μ = 7520.

Hₐ: The mean life of a large shipment of CFL bulbs is different from 7,520 hours, i.e. μ ≠ 7520.

The information provided is:

`\sigma=1200\\n=64\\\bar x=7324`

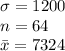
As the population standard deviation is provided, we will use a z-test for single mean.

Compute the test statistic value as follows:

`z=(\bar x-\mu)/(\sigma/√(n))=(7324-7520)/(1200/√(64))=-1.31`

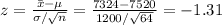
The test statistic value is -1.31.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected.

Compute the p-value for the two-tailed test as follows:

`p-value=2* P(Z<-1.31)\\=2* [1-P(Z<1.31)]\\=2* [1-0.90490]\\=0.1902`

*Use a z-table for the probability.

The p-value of the test is 0.1902.

The p-value of the test is very large for all the commonly used significance level. The null hypothesis will not be rejected.

Thus, it can be concluded that the mean life of a large shipment of CFL bulbs is equal to 7520 hours.