Question

A square plate RequalsStartSet (x comma y ): 0 less than or equals x less than or equals 1 comma 0 less than or equals y less than or equals 1 EndSet has a temperature distribution Upper T (x comma y )equals100 minus 25 x minus 40 y.

a. Sketch two level curves of the temperature in the plate.
b. Find the gradient of the temperature gradient Upper T (x comma y ).

Answer 1

Explanation:

We are given the following:

`R = \0\leq x \leq 1, 0 \leq y \leq 1 \`

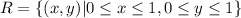
and
`T(x,y) = 100-25x - 40 y`

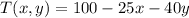
a). Recall that a level curve of a function f(x,y) is given by
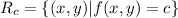`R_c = \(x,y)` where c is a constant. That is, all the points in the set of interest to which the function applied to the points is exactly the value c.

Consider c = 80. So we get

`100-25x-40y = 80`

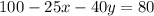
which implies that
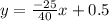`y = (-25)/(40)x+0.5`(Graph 1).

We can also consider c=60, which gives us

`100-25x-40y = 60`

which implies that
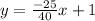`y = (-25)/(40)x+1`. (Graph 2)

b)Recall that the gradient of a function f(x,y) is given by

`\\abla f = ((df)/(dx), (df)/(dy))`

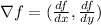
In this case,

`(dT)/(dx) = -25, (dT)/(dy) = -40`

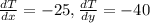
Thus, the gradient of T is given by

`\\abla T =(-25,-40)`