Question

A runner of mass 53.0 kg runs around the edge of a horizontal turntable mounted on a vertical, frictionless axis through its center. The runner's velocity relative to the earth has magnitude 3.60 m/s . The turntable is rotating in the opposite direction with an angular velocity of magnitude 0.200 rad/s relative to the earth. The radius of the turntable is 2.90 m , and its moment of inertia about the axis of rotation is 76.0 kg⋅m2

Answer 1

0.336 rad/s

Step-by-step explanation:

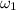`\omega_1` = Angular speed of the turntable = -0.2 rad/s

R = Radius of turntable = 2.9 m

I = Moment of inertia of turntable =
`76\ kgm^2`

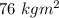
M = Mass of turn table = 53 kg

`v_1` = Magnitude of the runner's velocity relative to the earth = 3.6 m/s

As the momentum in the system is conserved we have

`Mv_1R+I\omega_1=(I + MR^2)\omega_2\\\Rightarrow \omega_2=(Mv_1R+I\omega_1)/(I + MR^2)\\\Rightarrow \omega_2=(53* 3.6-76* 0.2)/(76+53* 2.9^2)\\\Rightarrow \omega_2=0.336\ rad/s`

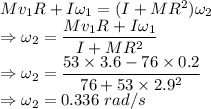
The angular velocity of the system if the runner comes to rest relative to the turntable which is the required answer is 0.336 rad/s