Question

1. A gambler makes 100 column bets at roulette. The chance of winning on any one play is 12/38. The gambler can either win $ 5 or lose $2 on each play.

a) Find the expected total amount of the gambler's win.
b) Find the standard deviation for the total amount of the gambler's win.
c) Use the normal distribution to estimate the probability that, in total, the gambler wins at least $1. (Note: Is it necessary to use the continuity correction? )

Answer 1

a) Expected amount of the gambler's win = $0.209

b) SD = 2.26

c)P (X >1) = P(z >0.35) = 0.36317

Explanation:

The probability of winning, p = 12/38 =6/19

Probability of losing, q = 1 -p = 1-6/19

q = 13/19

Win amount = $5

Loss amount = $2

a) Expected total amount of win = ((6/19)*5) - ((13/19)*2)

Expected total amount of win = 1.579 - 1.369

Expected amount of win, E(X) = $0.209

b) Standard Deviation for the total amount of the gambler's win

`SD = \sqrt{E(X^(2)) - (E(X))^(2) }`

E(X²) = (6/19)*5² - (13/19)*2²

E(X²) = 5.158

`SD = √(5.158 - 0.209^2)`

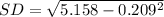
SD = 2.26

c) probability that, in total, the gambler wins at least $1.

P(X >1)

`z = (X - \mu)/(\sigma)`

μ = E(x) = 0.209

z = (1-0.209)/2.26

z = 0.35

P( X >1) = P(z >0.35)

P(z >0.35) = 1 - P(z <0.35)

P(z >0.35) = 1 - 0.63683

P(z >0.35) = 0.36317