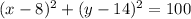Question

Ookmarks

GC
Equation of a Circle: Tutorial
Question
Points F(2,6) and G(14,22) are the endpoints of a diameter of circle M. What is the equation of circle M?

Answer 1

`(x - 8)^(2) + (y - 14)^(2) = 100`

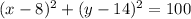
Explanation:

The equation of a circle has the following format:

`(x - x_(0))^(2) + (y - y_(0))^(2) = r^(2)`

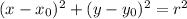
In which r is the radius(half the diameter) and the centre is the point
`(x_(0), y_(0))`

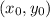
Points F(2,6) and G(14,22) are the endpoints of a diameter of circle M.

To find the diameter, we find the distance between these two points. So

`D = \sqrt{(14 - 2)^(2) + (22 - 6)^(2)} = \sqrt{12^(2) + 16^(2)} = 20`

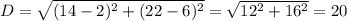
So

`r = (D)/(2) = 10`

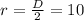
The centre is the midpoint between F and G. So

`x_(0) = (2 + 14)/(2) = 8`

`y_(0) = (6 + 22)/(2) = 14`

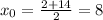
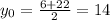
The equation is:

`(x - 8)^(2) + (y - 14)^(2) = 100`