Question

The radius of a right circular cylinder is increasing at a rate of 9.5 inches per minute and the height is decreasing at a rate of 11.5 inches per minute. What is the rate of change of the surface area when the radius is 16.5 inches and the height is 31 inches?

Answer 1

The rate of change of the surface area is 2,629 inches per minute.

Explanation:

Given that,

The height is decreasing at a rate of 11.5 inches per minute and the radius of a right circular cylinder is increasing at a rate of 9.5 inches per minute.

`(dr)/(dt)=9.5\ inches/min`

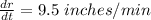
and

`(dh)/(dt)=-11.5 \ inches/min`

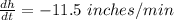
r = radius of the right circular cylinder

h= height of the right circular cylinder

The surface area of the right circular cylinder= 2π(r²+rh)

A=2π(r²+rh)

Differentiating with respect to t

`(dA)/(dt)=2\pi(2r(dr)/(dt)+r(dh)/(dt)+h(dr)/(dt))`

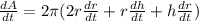
Now plug the value of
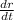`(dr)/(dt)` and
`(dh)/(dt)`.

`(dA)/(dt)=2\pi(2r* 9.5+r* (-11.5)+h* 9.5)`

`=2\pi(19r-11.5r+9.5h)`

`=2\pi(7.5r+9.5h)`

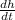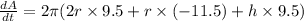
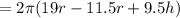
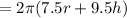
The rate of change of the surface area when the height is 31 inches and radius is 16.5 inches.

r = 16.5 inches, h = 31 inches

`(dA)/(dt)|_(r=16.5, h=31 )=2\pi (7.5 * 16.5+9.5* 31)`

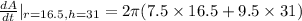
=2,629 inches per minute

The rate of change of the surface area is 2,629 inches per minute.