Answer:
x = ( 2a / b ) ^( 1 / 6 )
Step-by-step explanation:
Solution:-
- The The potential energy function for either one of the two atoms in a diatomic molecule is often approximated by:

Where, x : The separation between two atoms.
- We are to find the separation where the potential energy between two atoms is minimum. For that we have to resort to the methods of calculus. The given function U ( x ) is a single variable function of separation "x" which differential over all the real numbers interval.
- We will determine the first derivative of the potential energy function U ( x ) and set it to zero to calculate the critical values of separation x.
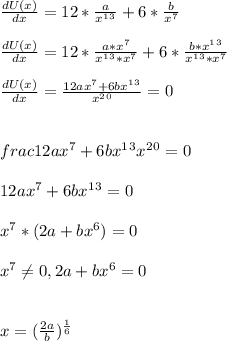
- The potential energy function U ( x ) has a local minima at x = ( 2a / b ) ^( 1 / 6 )