Answer:
a) 0.11% probability that the student will get exactly 6 answers correct
b) 94.37% probability of the student getting 3 or less answers correct
c) 5.63% probability of the student getting 4 or more answers correct
Explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
Suppose a student takes a multiple-choice exam composed of 8 questions with 5 possible answers to each question, exactly one of which is correct.
This means that

a) What is the probability that the student will get exactly 6 answers correct, which is necessary for a grade of 751 (5 points)
This is P(X = 6).

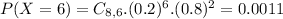
0.11% probability that the student will get exactly 6 answers correct
b) What is the probability of the student getting 3 or less answers correct? [5 points)
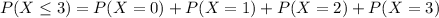

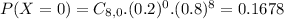

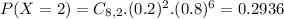
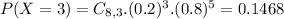

94.37% probability of the student getting 3 or less answers correct
c) What is the probability of the student getting 4 or more answers correct? [Hint: the complement of this event is getting 3 or less answers
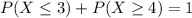
We want
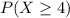
So

5.63% probability of the student getting 4 or more answers correct