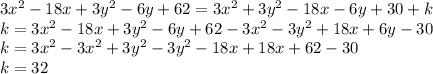Answer:
k=32
Explanation:
Given the points:
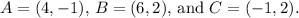
The first step is to find the Centroid of the triangle.
Centroid, X
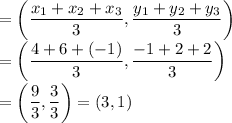
Next, let P be a point (x,y)
Using the distance formula,
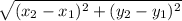
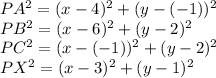
On Substitution into:
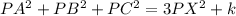
![(x-4)^2+(y-(-1))^2+(x-6)^2+(y-2)^2+(x-(-1))^2+(y-2)^2=3[(x-3)^2+(y-1)^2]+k](https://img.qammunity.org/2021/formulas/mathematics/middle-school/h9reknebvi2l6agkoujl9okwjv3y60ryze.png)
Let us simplify the LHS first
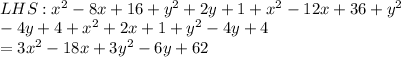
Also, the Right Hand Side
![RHS:3[(x-3)^2+(y-1)^2]+k\\=3[x^2-6x+9+y^2-2y+1]+k\\=3x^2-18x+27+3y^2-6y+3+k\\=3x^2+3y^2-18x-6y+30+k](https://img.qammunity.org/2021/formulas/mathematics/middle-school/cxltvn582f00qfbbx8yfj0i2tz80q4z7jy.png)
Therefore: