Question

A doctor is measuring the mean systolic blood pressure of female students at a large college. Systolic blood pressure is known to have a skewed distribution. The doctor collects systolic blood pressure measurements from random sample of 28 female students. The resulting 90% confidence interval is (100.4, 159.6). Units of systolic blood pressure are mmHg.

1. Which one of the following conclusions is valid?
Group of answer choices:
a. 90% of the female students at the college have a systolic blood pressure between 100.4 mmHg and 159.6 mmHg.
b. The sampling distribution of means will probably not follow a normal distribution, so we cannot draw a conclusion.
c. We are 90% confident that the mean systolic blood pressure for female students at the college is between 100.4 mmHg and 159.6 mmHg.

Answer 1

The correct option is (b).

Explanation:

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha/2)*(SD)/(√(n))`

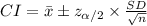
The confidence interval for population mean can be computed using either the z-interval or t-interval.

The t-interval is used if the following conditions are satisfied:

• The population standard deviation is not known
• The sample size is large enough
• The population from which the sample is selected is normally distributed.

For computing a (1 - α)% confidence interval for population mean , it is necessary for the population to normally distributed if the sample selected is small, i.e.n < 30, because only then the sampling distribution of sample mean will be approximated by the normal distribution.

In this case the sample size is, n = 28 < 30.

Also it is provided that the systolic blood pressure is known to have a skewed distribution.

Since the sample is small and the population is not normally distributed, the sampling distribution of sample mean will not be approximated by the normal distribution.

Thus, no conclusion can be drawn from the 90% confidence interval for the mean systolic blood pressure.

The correct option is (b).