Answer:
D
Explanation:
The average rate of change of a function over an interval a ≤ x ≤ b is found by:
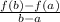
Here, a is 0 and b is 3, so:

Just plug in 3 for the first term and 0 for the second term in the numerator:
- First term:
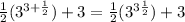
- Second term:

So, the final answer is:
![\frac{[(1)/(2) (3^{3(1)/(2) })+3]-[(1)/(2) (3^{(1)/(2) })+3]}{3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/jz7chsc6w7wn5v12idkrqnc9svx4c164nl.png)
Thus, the answer is D.
Hope this helps!