Question

The energy efficiency of an incandescent light bulb (= the percentage of consumed power that is actually converted into radiated light) is typically around 5%. Suppose a certain brand of 75 W incandescent bulb emits light primarily at wavelength ???? = 570 nm.

Calculate the total number of photons emitted by one of those bulbs if it has been shining for a 6-hour period.

Answer 1

4*10^22 photons

Step-by-step explanation:

To find the number of photons is necessary to calculate the total energy of the light emitted in one hour = 3600s:

`E'=0.05E=0.05Pt=0.05(75J/s)(3600s)=13.500J`

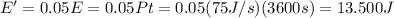
Furthermore, is necessary to find the associated energy to the photon 0f 570nm with following formula:

`E'=h\\u=h(c)/(\lambda)`

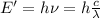
h: Planck's constant = 6.62*10^-34 Js

c: speed of light = 3*10^8 m/s

wavelength = 570*10^-9 m

`E_p=(6.62*10^(-34)Js)(3*10^(8)m/s)/(570*10^(-9)m)=3.484*20^(-29)J`

Finally you divide E' between Ep to find the number of photons:

`n=(E')/(E_p)=(13.500J)/(3.484*10^(-19))\approx4*10^(22)photons`

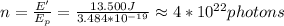
the number of emitted photons is 4*10^22