Answer:
Part (a)
see attached for sample space
Part (b)

Total number of possible outcomes = 12

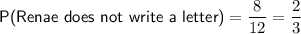

Part (c)
Her activity does not depend on which bus she takes, as we have been told that once she is on the bus, she randomly selects the activity. Therefore, the activity selection is independent from the bus selection.
The sample space confirms this as it shows that the probability of the selecting each activity is equally likely for each of the 4 buses.