Question

The ELISA test was an early test used to screen blood donations for antibodies to HIV. A study (Weiss et al. 1985) found that the conditional probability that a person would test positive given they have HIV was 0.979 and the conditional probability that a person would test negative given they did not have HIV was 0.919. The World Almanac gives an estimate of the probability of a person 15 years or older in the United States of America having HIV of 0.005.Suppose a random person is tested and they test positive. What is the conditional probability that this person has HIV given that they test positive

Answer 1

0.057258

Explanation:

From the statement of the problem, the following information were given:

• P(Positive|HIV)=0.979
• P(Negative|No HIV)=0.919
• P(HIV)=0.005

The following can be derived:

• P(Positive|No HIV)=1-P(Negative|No HIV)=1-0.919=0.081
• P(No HIV)=1-P(HIV)=1-0.005=0.995

We are to determine the probability that a person has HIV given that they test positive. [P(HIV|Positive)]

Using Baye's theorem for Conditional Probability

`P(HIV|Positive)=(P(Positive|HIV)P(HIV))/(P(Positive|HIV)P(HIV)+P(Positive|No HIV)P(No HIV))`
`=(0.979*0.005)/(0.979*0.005+0.081*0.995)`

`P(HIV|Positive)=0.057258`

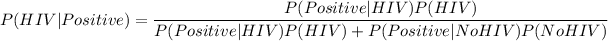
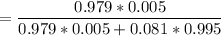
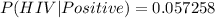
The probability that a random person tested has HIV given that they tested positive is 0.057258.