Answer
(a)
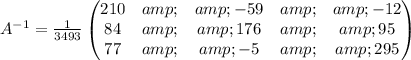
(b)
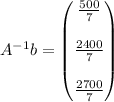
Explanation:
Remember that when you want to solve a problem like this, you express the equation as following
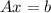
So, if you know the inverse of
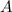 then
then
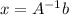
For this case
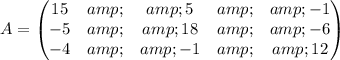
Now for this case the inverse of A would be
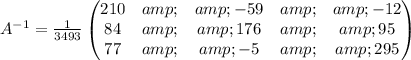
Then when you multiply with the vector solution

So from that information you can conclude that the solution to the system of equations is x = 500/7 y = 2400/7 and z = 2700/7