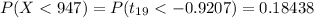Question

Twenty weather stations are deployed on Mars, at diverse locations. A normal plot shows that it is reasonable to assume that weather station lifetimes are approximately normally distributed. (Weather station lifetime is how long the station operates before breaking down.) The sample average lifetime is 947 Martian days, and the sample standard deviation of lifetimes is 136 days. If the true mean lifetime of a weather station is 975 Martian days.

a. What is the probability the sample mean is 947 days or less?
b. What sampling distribution should we use to compute this probability?

Answer 1

a) P(Xs<947)=0.1844

b) The sampling distribution has to be evaluated with the t-students distribution, as the population standard deviation is not known.

Explanation:

We have a sample of n=20 weather stations, with a sample average lifetime of 947 days and a sample standard deviation of s=136 days.

The population mean lifetime is 975 days.

We have to calculate the probability of having a sample with mean of 947 days or less, given that the population mean is 975 days.

As the population standard deviation is unknown, we will use the t-value and estimate the population standard deviation with the sample standard deviation.

The t-value for a X=947 is:

`t=(X-\mu)/(s/√(n))=(947-975)/(136/√(20))=(-28)/(30.4105)=-0.9207`

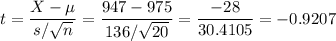
The degrees of freedom are:

`df=n-1=20-1=19`

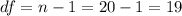
We can now calculate the probability of having a sample with mean of 947 days or less:

`P(X<947)=P(t_(19)<-0.9207)=0.18438`