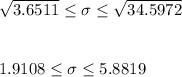Question

The amount of lateral expansion (mils) was determined for a sample of n = 8 pulsed-power gas metal arc welds used in LNG ship containment tanks. The resulting sample standard deviation was s = 2.89 miles. Assuming normality, derive a 95% CI for? 2 and for?

Answer 1

95% Confidence interval for the variance:

`3.6511\leq \sigma^2\leq 34.5972`

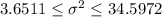
95% Confidence interval for the standard deviation:

`1.9108\leq \sigma \leq 5.8819`

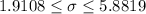
Explanation:

We have to calculate a 95% confidence interval for the standard deviation σ and the variance σ².

The sample, of size n=8, has a standard deviation of s=2.89 miles.

Then, the variance of the sample is

`s^2=2.89^2=8.3521`

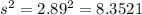
The confidence interval for the variance is:

`( (n - 1) s^2)/( \chi_(\alpha/2)^2) \leq \sigma^2 \leq ( (n - 1) s^2)/(\chi_(1-\alpha/2)^2)`

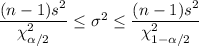
The critical values for the Chi-square distribution for a 95% confidence (α=0.05) interval are:

`\chi_(0.025)=1.6899\\\\\chi_(0.975)=16.0128`

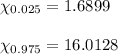
Then, the confidence interval can be calculated as:

`( (8 - 1) 8.3521)/( 16.0128) \leq \sigma^2 \leq ( (8 - 1) 8.3521)/(1.6899)\\\\\\3.6511\leq \sigma^2\leq 34.5972`

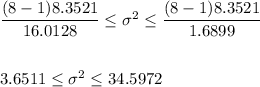
If we calculate the square root for each bound we will have the confidence interval for the standard deviation:

`√(3.6511)\leq \sigma\leq √(34.5972)\\\\\\1.9108\leq \sigma \leq 5.8819`