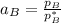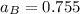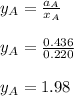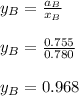Answer:
Step-by-step explanation:
From the knowledge of liquid and vapor phases
 is the mole fraction in the liquid
is the mole fraction in the liquid
 is the mole fraction in the vapor
is the mole fraction in the vapor
Given that :
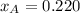
 = 0.314
= 0.314
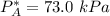
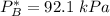
using the formula:
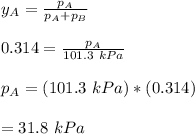
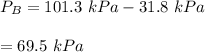
To calculate the activities and activity coefficients of both components in the solution; we have: