Answer:
V=16
Explanation:
We are given that an inverse variation
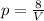
We have to find the value of V when p=1/2
To find the value of V we will substitute the value of p
Substitute the value of p
Then, we get
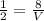
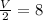
Using multiplication property of equality
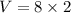
Using multiplication property of equality
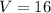
Hence, the value of V=16