Answer:
b) next three terms of the sequence are 47, 51, 55
c) The next three terms are 1100, 1101, 1110
d) The next three items in the sequence are therefore, 8,8,8
f) The next three terms are 654729075, 13749310575, 316234143225
g) Therefore the next three items in the sequence are 0,0,0
Explanation:
b)7, 11, 15, 19, 23, 27, 31, 35, 39, 43, ...
the common difference, d =
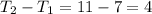
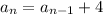
43 + 4 = 47
47 + 4 = 51
51 + 4 = 55
next three terms of the sequence are 47, 51, 55
c) 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011,...
Each of these terms are binary numbers of 1,2,3,4........
The 1st next term is the 12th term = 1100₂
The second next term is the 13th term = 1101₂
The third next term is the 14th term = 1110₂
The next three terms are 1100, 1101, 1110
d) 1, 2, 2, 2, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, ...
1 is repeated 1 time , 2 is repeated 3 times, 3 is repeated 5 times, 5 is repeated 7 times, the next number will sure be repeated 9 times( the repetition follows an odd number pattern)
To know the next number that will be repeated 9 times:
1+2 = 3
2+3 = 5
3 + 5 = 8
The pattern is that the previous summation adds to the preceding number
The next three items in the sequence are therefore, 8,8,8
f) 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425,...
The above sequence follows the pattern
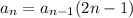
The next three terms are the 10th, 11th and 12th terms
a₁₀ = 34459425((2*10)-1)
a₁₀ = 654729075
a₁₁ = 654729075((2*11)-1)
a₁₁ = 13749310575
a₁₂ = 13749310575((2*12)-1)
a₁₂ = 316234143225
The next three terms are 654729075, 13749310575, 316234143225
g) 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1,...
The sequence changes between 1 and 0. 6 zeros are expected next
Therefore the next three items in the sequence are 0,0,0