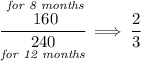Question

. Mrs. Rojas deposited $8000 into an account paying 4% interest annually. After 8 months Mrs. Rojas withdrew the $6000 plus interest. Altogether, how much money did Mrs. Rojas withdraw? What fraction of a year's interest was earned? 760​

Answer 1

well, keeping in mind that a year has 12 months, that means that 8 months is 8/12 of a year, when Mrs Rojas pull her money out.

`~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$6000\\ r=rate\to 4\%\to (4)/(100)\dotfill &0.04\\ t=years\to (8)/(12)\dotfill &(2)/(3) \end{cases} \\\\\\ A=6000[1+(0.04)((2)/(3))]\implies A=6000\left( (77)/(75) \right)\implies A=6160`

well, she put in 6000 bucks, got back 160 extra, that's the interest earned in the 8 months.

what if she had left her money for 1 whole year, then

`~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$6000\\ r=rate\to 4\%\to (4)/(100)\dotfill &0.04\\ t=years\dotfill &1 \end{cases} \\\\\\ A=6000[1+(0.04)(1)]\implies A=6240`

so had she left it in for a year, she'd have gotten 6240, namely 240 in interest, well, what fraction of a year's interest was earned? or worded differently, what fraction is 160(8 months) of 240(1 year)?

`\cfrac{\stackrel{\textit{for 8 months}}{160}}{\underset{\textit{for 12 months}}{240}}\implies \cfrac{2}{3}`