Question

Kellogg is planning to market a new kind of cereal. However, before marketing this product, the company wants to find what percentage of people will like it. The company’s research department selected a random sample of 500 persons and asked them to taste it. Of these 500 persons, 280 said they liked it. Set up a 95% confidence interval estimate of the proportion of all people who like this cereal. Kellogg will market the cereal if at least half of the people in the population will like it. Based on the sample results, should Kellogg market the cereal? What is the predominant formula you will use to solve the problem?

Answer 1

The predominant formula that will be used to solve the problem is,

`CI=\hat p\pm z_(\alpha/2)*\sqrt{(\hat p(1-\hat p))/(n)}`.

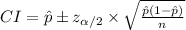Explanation:

Kellogg is planning to market a new kind of cereal and wants to determine the percentage of people will like it.

Kellogg will market the cereal if at least half of the people in the population will like it.

So, the company’s research department selected a random sample of 500 persons and asked them to taste it. Of these 500 persons, 280 said they liked it.

The hypothesis to test whether Kellogg will market the cereal is:

H₀: Kellogg will not market the cereal, i.e. p < 0.50.

Hₐ: Kellogg will market the cereal, i.e. p ≥ 0.50.

The decision rule:

A 95% confidence interval for single proportion can be used to draw conclusion about this test.

If the 95% confidence interval consists of the null value, i.e. p < 0.50, then the null hypothesis will not be rejected. But is the confidence interval does not consist of the null value then the null hypothesis will be rejected.

The formula to compute the 95% confidence interval for the proportion of all people who like this cereal is:

`CI=\hat p\pm z_(\alpha/2)*\sqrt{(\hat p(1-\hat p))/(n)}`

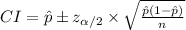
Here,

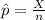`\hat p=(X)/(n)` = sample proportion

`z_(\alpha/2)` = critical value of z for α = 0.05

Thus, the predominant formula that will be used to solve the problem is,

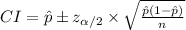`CI=\hat p\pm z_(\alpha/2)*\sqrt{(\hat p(1-\hat p))/(n)}`.