Question

Determine the decision criterion for rejecting the null hypothesis in the given hypothesis​ test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis. We wish to compare the means of two populations using paired observations. Suppose that d overbar equals​3.125, subscript dequals​2.911, and nequals​8, and that you wish to test the following hypothesis at the​ 10% level of significance. H0​: mu Subscript d equals 0 against H1​: muSubscript dgreater than0 What decision rule would you​ use?

Answer 1

`t = (3.125-0)/((2.911)/(√(8)))= 3.036`

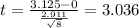
We can use the p value as a decision rule is
`p_v<\alpha` we reject the null hypothesis.

Now we can find the degrees of freedom given by:

`df = n-1=8-1=7`

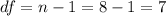
And the p value would be:

`p_v = P(t_(7) >3.036) = 0.0094`

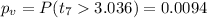
And since the
`p_v <\alpha` we have enough evidence to reject the null hypothesis in favor to the alternative hypothesis.

Explanation:

For this case we have the following statistics for the difference between the paired observations:

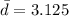`\bar d = 3.125` the sample mean for the paired difference

`s_d = 2.911` the sample deviation for the paired difference data

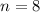`n =8` the sample size

The system of hypothesis that we want to check is:

Null hypothesis:
`\mu_d =0`

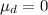
Alternative hypothesis:
`\mu_d > 0`

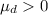
And the statistic is given by:

`t = (\bar d -\mu_d)/((s_d)/(√(n)))`

And replacing we got:

`t = (3.125-0)/((2.911)/(√(8)))= 3.036`

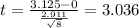
We can use the p value as a decision rule is
`p_v<\alpha` we reject the null hypothesis.

Now we can find the degrees of freedom given by:

`df = n-1=8-1=7`

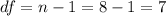
And the p value would be:

`p_v = P(t_(7) >3.036) = 0.0094`

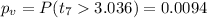
And since the
`p_v <\alpha` we have enough evidence to reject the null hypothesis in favor to the alternative hypothesis.