Question

Vitamin​ D, whether ingested as a dietary supplement or produced naturally when sunlight falls upon the​ skin, is essential for​ strong, healthy bones. The bone disease rickets was largely eliminated during the​ 1950s, but now there is concern that a generation of children more likely to watch TV or play computer games than spend time outdoors is at increased risk. A recent study of 3400 children randomly selected found 24​% of them deficient in vitamin D.

a) Find a 98% confidence interval.
b) Explain carefully what your interval means.
c) Explain what "98% confidence" means.

Answer 1

a)
`0.24 - 2.33\sqrt{(0.24(1-0.24))/(3400)}=0.223`

`0.24 + 2.33\sqrt{(0.24(1-0.24))/(3400)}=0.257`

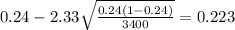
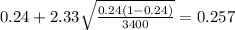
The 98% confidence interval would be given by (0.223;0.257)

b) This interval establish the limits on where we can expect the true value for the population proportion with deficient in vitamin D at 98% of confidence

c) The 98% represent the confidence level for the interval founded so we have a probability of 2% of comit error Type I.

Explanation:

Part a

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. The confidence level is at 98% of confidence, our significance level would be given by
`\alpha=1-0.98=0.02` and
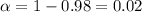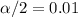`\alpha/2 =0.01`. And the critical value would be given by:

`z_(\alpha/2)=-2.33, z_(1-\alpha/2)=2.33`

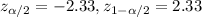
The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

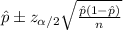
If we replace the values obtained we got:

`0.24 - 2.33\sqrt{(0.24(1-0.24))/(3400)}=0.223`

`0.24 + 2.33\sqrt{(0.24(1-0.24))/(3400)}=0.257`

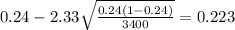
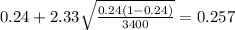
The 98% confidence interval would be given by (0.223;0.257)

Part b

This interval establish the limits on where we can expect the true value for the population proportion with deficient in vitamin D at 98% of confidence

Part c

The 98% represent the confidence level for the interval founded so we have a probability of 2% of comit error Type I.