Question

Surgery is in 4 out if every 10 hospital emergency room visits. If a large urban hospital had 840 emergency visits in the past month how many of these visits would you expect to required surgery

Answer 1

Expected number of visits to the emergency room that would require a surgery is 336.

Explanation:

Let X = number of surgery.

The odds of having a surgery in a randomly selected visit to a emergency room is 4 out of 10.

Then the probability of having a surgery in a randomly selected visit to a emergency room is:

`p=(4)/(10)=0.40`

In the past month a large urban hospital had 840 emergency visits.

An emergency room visit may lead to surgery or not is independent of the others.

The random variable X follows a Binomial distribution with parameters n = 840 and p = 0.40.

The expected value of a binomial random variable is:

`E(X)=np`

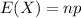
Compute the expected number of visits that would require a surgery as follows:

`E(X)=np`

`=840* 0.40\\=336`

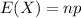
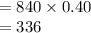
Thus, expected number of visits to the emergency room that would require a surgery is 336.