Question

Fairfield Homes is developing two parcels near Pigeon Fork, Tennessee. In order to test different advertising approaches, it uses different media to reach potential buyers. The mean annual family income for 14 people making inquiries at the first development is $150,000, with a standard deviation of $43,000. A corresponding sample of 27 people at the second development had a mean of $186,000, with a standard deviation of $27,000. Assume the population standard deviations are the same.

1. State the decision rule for .01 significance level: H0: μ1 = μ2; H1:μ1 ≠ μ2. (Negative amounts should be indicated by a minus sign. Round your answers to 3 decimal places.)

- Reject H0 if t is not between__________and__________.

2. Compute the value of the test statistic. (Negative amount should be indicated by a minus sign. Round your answer to 2 decimal places.)

- Value of the test statistic__________

Answer 1

(1) Reject
`H_0` if t is not between -2.708 and 2.708.

(2) The value of the test statistic is -3.29.

Explanation:

We are given that the mean annual family income for 14 people making inquiries at the first development is $150,000, with a standard deviation of $43,000. A corresponding sample of 27 people at the second development had a mean of $186,000, with a standard deviation of $27,000.

Let
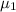`\mu_1` = mean annual family income at the first development

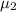`\mu_2` = mean annual family income at the second development

SO, Null Hypothesis,
`H_0` :
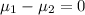`\mu_1-\mu_2=0` or
`\mu_1= \mu_2`

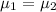
Alternate Hypothesis,
`H_A` :
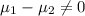`\mu_1-\mu_2\\eq 0` or
`\mu_1\\eq \mu_2`

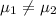
The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n__1+_n__2-2`

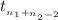
where,
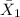`\bar X_1` = sample mean annual family income for people making inquiries at the first development = $150,000

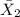`\bar X_2` = sample mean annual family income for people making inquiries at the second development = $186,000

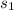`s_1` = sample standard deviation for people making inquiries at the first development = $43,000

`s_2` = sample standard deviation for people making inquiries at the second development = $27,000

`n_1` = sample of people making inquiries at the first development = 14

`n_2` = sample of people making inquiries at the second development = 27

Also,
`s_p=\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
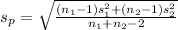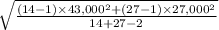`\sqrt{((14-1)* 43,000^(2)+(27-1)* 27,000^(2) )/(14+27-2) }` = 33,201.41

(1) The decision rule for the given hypothesis at 0.01 significance level is;

• If the value of test statistics lies within the range of critical values of t at 39 degree of freedom of -2.708 and 2.708, then we will not reject our null hypothesis as it will not fall in the rejection region.

• If the value of test statistics does not lie within the range of critical values of t at 39 degree of freedom of -2.708 and 2.708, then we will reject our null hypothesis as it will fall in the rejection region.

So, Reject
`H_0` if t is not between -2.708 and 2.708.

Now, the test statistics =
`\frac{(150,000-186,000)-(0)}{33,201.41 * \sqrt{(1)/(14)+(1)/(27) } }` ~
`t_3_9`

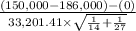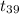
= -3.29

(2) Hence, the value of the test statistic is -3.29.