Question

A professor wishes to discover if seniors skip more classes than freshmen. Suppose he knows that freshmen skip 2% of their classes. He randomly samples a group of seniors and out of 2521 classes, the group skipped 77.

1. Based on the sample, does it appear that seniors skip more than 2% of their classes?
2. State the critical value (CV), test statistic (TS), and decision from the test. (Use α = 0.01.)

Answer 1

We conclude that seniors skip more than 2% of their classes at 0.01 level of significance.

Explanation:

We are given that a professor wishes to discover if seniors skip more classes than freshmen. Suppose he knows that freshmen skip 2% of their classes.

He randomly samples a group of seniors and out of 2521 classes, the group skipped 77.

Let p = percentage of seniors who skip their classes.

So, Null Hypothesis,
`H_0` : p
`\leq` 2% {means that seniors skip less than or equal to 2% of their classes}

Alternate Hypothesis,
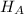`H_A` : p > 2% {means that seniors skip more than 2% of their classes}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
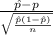`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
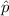`\hat p` = sample proportion of seniors who skipped their classes =
`(77)/(2521)`

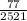
n = sample of classes = 2521

So, test statistics =
`\frac{(77)/(2521) -0.02}{{\sqrt{((77)/(2521)(1-(77)/(2521)))/(2521) } } } }`

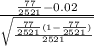
= 3.08

The value of the test statistics is 3.08.

Now at 0.01 significance level, the z table gives critical value of 2.3263 for right-tailed test. Since our test statistics is more than the critical value of z as 2.3263 < 3.08, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that seniors skip more than 2% of their classes.