Question

Consider two protons that are separated by 5.9 fm. What is the magnitude of the Coulomb repulsive force between them?

Assume that these protons are on opposite sides of a nucleus and that the strong force on their nearest neighbors is about 2000 N, but nearly zero between nucleons on opposite sides of the nucleus.

Answer 1

F = 6.604N

Step-by-step explanation:

To find the electric force between the protons you use the Coulomb's formula:

`F=k(q_1q_2)/(r^2)=k(q^2)/(r^2)`

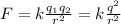
where you have used that both charges have the same charge.

K: Coulomb's constant = 8.98*10^9 Nm^2/C^2

r: distance between the charges = 5.9fm = 5.9*10^{-15}m

q: 1.6*10^{-19}C

By replacing the values of k, q and r you obtain:

`F=(8.98*10^9Nm^2/A^2)((1.6*10^(-19)C)^2)/((5.9*10^(-15)m)^2)=6.604N`

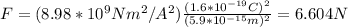
If you compare this force with the nuclear one Fn = 2000N you obtain:

`(F_n)/(F)=(2000N)/(6.604N)=302.8`

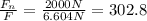
hence, the nuclear force is about 302.8 times stronger than the Coulomb's force

Answer 2

Assuming that these protons are on opossite sides of a nucleus, the strong force between them is zero. The magnitude of the repulsive force between them is given by:

`F=k(e^2)/(d^2)`

Where k is the coulomb constant, e is the proton charge and d its distance of separation. Replacing the given values and solving:

`F=8.99*10^(9)(N\cdot m^2)/(C^2)((1.6*10^(-19)C)^2)/((5.9*10^(-15)m)^2)\\F=6.61N`