Answer:
(a) The proportion of tenth graders reading at or below the eighth grade level is 0.1673.
(b) The 95% confidence interval for the population proportion of tenth graders reading at or below the eighth grade level is (0.198, 0.260).
Explanation:
Let X = number of students who read above the eighth grade level.
(a)
A sample of n = 269 students are selected. Of these 269 students, X = 224 students who can read above the eighth grade level.
Compute the proportion of students who can read above the eighth grade level as follows:
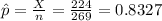
The proportion of students who can read above the eighth grade level is 0.8327.
Compute the proportion of tenth graders reading at or below the eighth grade level as follows:
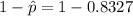
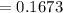
Thus, the proportion of tenth graders reading at or below the eighth grade level is 0.1673.
(b)
the information provided is:
n = 709
X = 546
Compute the sample proportion of tenth graders reading at or below the eighth grade level as follows:
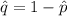
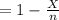
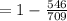

The critical value of z for 95% confidence interval is:
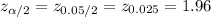
Compute the 95% confidence interval for the population proportion as follows:
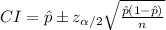
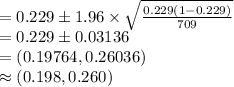
Thus, the 95% confidence interval for the population proportion of tenth graders reading at or below the eighth grade level is (0.198, 0.260).