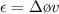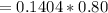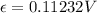Answer:
The maximum change in flux is
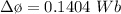
The average induced emf
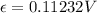
Step-by-step explanation:
From the question we are told that
The speed of the technician is
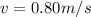
The distance from the scanner is
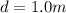
The initial magnetic field is
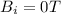
The final magnetic field is
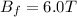
The diameter of the loop is
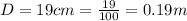
The area of the loop is mathematically represented as
![A = \pi [(D)/(2) ]^2](https://img.qammunity.org/2021/formulas/physics/college/7h4mdjehps4zgg08vb9uwqfoasm1rn3i23.png)
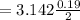
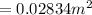
At maximum the change in magnetic field is mathematically represented as
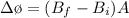
=>
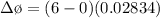
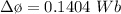
The average induced emf is mathematically represented as